Graph Chromatic Numbers
The chromatic number $ \chi(G) $ for a graph G = (V, E) signifies the minimum colors required to paint the graph’s vertices in such a way that no adjacent vertices share the same color.
This concept boils down to finding the smallest palette that ensures adjacent vertices are never colored identically.
A graph's coloring involves a function f: V → C, assigning a unique color to each vertex.
The chromatic number of G, represented as χ(G), indicates the fewest colors needed for a graph to be colored properly.
Determining a graph's chromatic number can be a significant computational challenge. Although various algorithms aim to estimate or pinpoint this number, the coloring dilemma for some graphs falls into the category of NP-complete problems.
Examples
Take, for instance, a bipartite graph, where the chromatic number is neatly $ \chi(G) = 2 $.
Here, it's clear that no vertex shares an edge with another of the same color, illustrating the principle of chromatic numbers perfectly.
"Adjacent vertex" here refers to two vertices connected directly by an edge.
For bipartite graphs, the chromatic number invariably stands at 2. This stems from the fact that no edges connect vertices within the same subset, allowing a single color to uniformly cover all vertices in one independent set.
Example 2
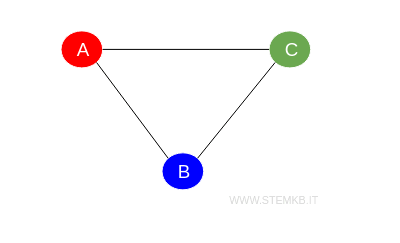
Consider the triangle graph, or \(C_3\), a simple 3-vertex cycle, to demonstrate a graph requiring three colors to ensure adjacent vertices don't match in color.
This scenario is among the simplest for non-bipartite graphs.
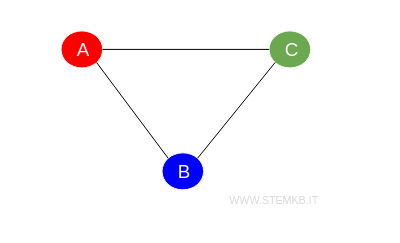
Here, the chromatic number is $ \chi(G) = 3 $, necessitating three distinct colors due to each vertex's adjacency to the others.
The color distribution could be A in red, B in blue, and C in green, ensuring distinct colors for adjacent vertices.
Example 3
Another graph presents a chromatic number of $ \chi(G) = 3 $, further exemplifying the concept.
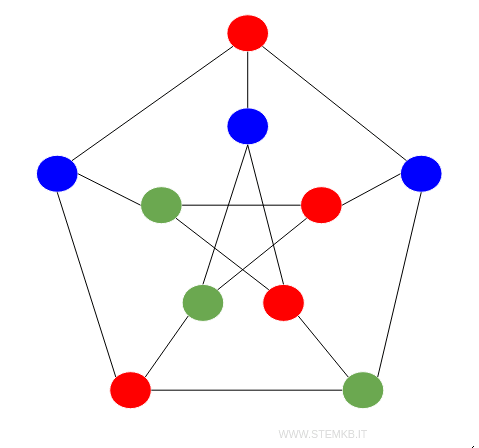
Once again, each adjacent vertex showcases a different hue.
The Chromatic Number's Utility
The practical applications of chromatic numbers are widespread and diverse.
Its use in cartography, for instance, aids in delineating maps clearly to avoid confusion among adjacent regions.
Beyond mapping, this concept plays a crucial role in computational theory for analyzing algorithms and solving problems related to scheduling and resource allocation.
FAQs
- Does a bipartite graph always have a chromatic number of 2?
Absolutely. In the case of bipartite graphs, their chromatic number is invariably 2. This stems from the ability to assign one color to all vertices in one subset and a different color to those in the opposite subset, effectively preventing any two neighboring vertices from sharing the same color. - Is a graph automatically considered k-partite if its chromatic number is k?
Not exactly. While there's a relationship between the notion of a k-partite graph and its chromatic number \( \chi{(G)} \), they are not synonymous. Thus, a graph with a chromatic number \( \chi{(G)}=k \) doesn't automatically qualify as k-partite. - Is the chromatic number of a graph with n vertices always within the range of 1 to n?
Indeed, the chromatic number for a graph harboring \(n\) vertices consistently falls between 1 and \(n\). The lower bound, 1, is observed in graphs that are entirely disconnected, allowing the same color for all vertices. Conversely, the upper limit, \(n\), manifests in a fully connected graph, necessitating distinct colors for each vertex to maintain the adjacent vertices' color disparity. - Is the chromatic number of a graph containing an odd cycle at least 3?
Yes, the existence of an odd cycle within a graph precludes it from being colored with merely two colors, thus elevating the chromatic number to a minimum of 3. This is illustrated by the simplest odd cycle, a triangle, where after two adjacent vertices are colored distinctly, it becomes impossible to color the third without duplicating one of the previously used colors, given its adjacency to both.
