K-Partite Graphs
A graph qualifies as a k-partite graph when its vertices can be neatly divided into k non-overlapping subsets, known as partitions or classes.
These subsets are disjoint (mutually exclusive), meaning edges can only connect vertices from different subsets, effectively preventing any connections within the same subset.
This arrangement ensures that each edge acts as a bridge between distinct subsets, with every vertex finding its place in one unique partition.
Expanding on the bipartite graph concept, k-partite graphs take the idea further by dividing vertices into k disjoint sets, unlike bipartite graphs that only use two. This structure means that connections only occur between distinct sets, prohibiting any intra-set edges.
Simply put, k-partite graphs categorize vertices into k distinct groups, allowing for connections exclusively between differing groups, thereby eliminating the possibility of connections within the same group.
Case Study: A Simple Scenario
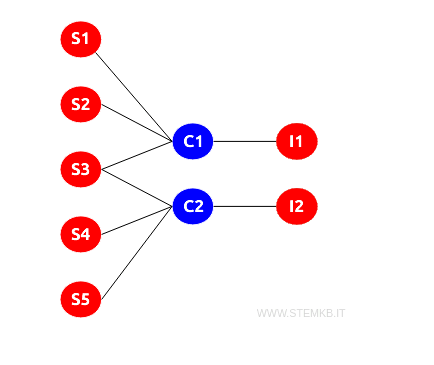
Consider a scenario with three distinct entity types: `Students`, `Courses`, and `Teachers`.
This situation is perfectly modeled by a tripartite graph, or a graph where k=3 (3-partite graph), illustrated as follows:
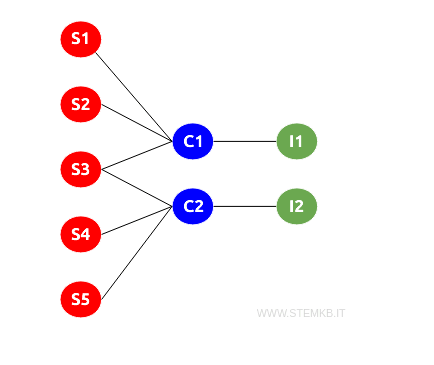
Here, the set {S1, S2, S3, S4, S5} represents five students, the set {C1, C2} includes two courses, and the set {I1, I2} represents two teachers.
- Connections between `Students` and `Courses` indicate the courses each student is taking.
- Connections between `Courses` and `Teachers` (e.g., C1-I1, C2-I2) show which teacher is responsible for each course.
For example, one student (S3) is enrolled in both courses C1 and C2, showcasing the flexible modeling capabilities of k-partite graphs. Each course is linked to a specific teacher, ensuring clear and organized representation.
This tripartite graph framework prohibits edges between vertices within the same subset. Thus, direct connections among students, courses, or teachers are absent, maintaining clear demarcations between different entity types.
The chromatic number of a k-partite graph is capped at k, enabling a unique color for each subset to prevent adjacent vertices from sharing the same color.
The Utility of K-Partite Graphs
K-partite graphs are instrumental across a broad spectrum of applications requiring nuanced modeling of interrelations among diverse object or entity types. Their structure lends itself well to complex scheduling, efficient resource allocation, and sophisticated recommendation system design, among other uses.
FAQ
- Is the chromatic number of a k-partite graph always k?
The assumption that a k-partite graph automatically has a chromatic number equal to k is a common misconception. In reality, the chromatic number of such a graph is capped at k, but can fall below this threshold if, for example, any of the k separate sets can share a color without contravening the principles of graph coloring. When it comes to bipartite graphs, a specific subset where k=2, they exhibit a chromatic number of 2 provided there is at least one edge; absent any edges, the chromatic number drops to 1.
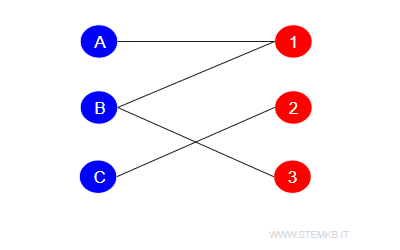
For graphs where k exceeds 2, determining the chromatic number becomes more nuanced, relying heavily on the graph's unique configuration and how its vertices interconnect. Take, for instance, a graph that is tripartite with k=3; its chromatic number might only be 2 despite the potential for more complexity.